Both Artificial Intelligence (AI) and Quantum Computing (QC) heavily rely on Linear Algebra as their primary calculation tool.
Linear algebra finds numerous applications across scientific, engineering, and computing disciplines. The following diagram illustrates the relationships between various topics of Linear Algebra for AI and Quantum Computing. This article discusses the first four topics (Vectors, Matrices, Tensors, and Product Rules), while the remaining topics (Decomposition, Advanced Concepts for Quantum Computing, Matrix Calculus for Machine Learning, and Deep Learning) will be covered in subsequent articles.
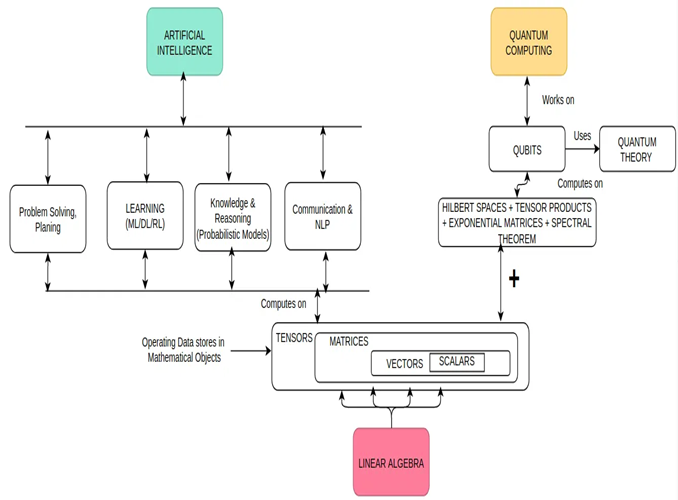
Linear Algebra addresses this issue by initially storing your data in vectors, matrices, and tensors, and then performing computations based on your instructions. In simple terms, linear algebra serves as a foundation.
Clustering, data fitting, classification, validation, and feature engineering represent just a few of the Machine Learning and AI applications of Linear Algebra.
Principal component analysis (PCA), non-negative matrix factorization, and advanced clustering methods are all examples of linear algebra’s application in unsupervised learning techniques, such as k-means. Techniques for computing model parameters and other forms of regression and classification, such as logistic regression and the support vector machine, can be applied to problems of considerable complexity.
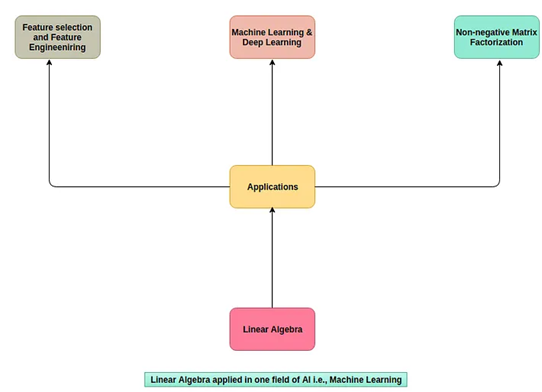
Machine Learning is a branch of artificial intelligence that employs linear algebra in data fitting, feature selection, and engineering.
In contrast to classical computers (desktops and laptops), which rely on Newtonian physics, the new computational model underlying quantum computing is grounded in the laws of nature and the cosmos. Complex linear algebra concepts such as the Tensor Product, Decomposition, Spectral Theorem, and Matrix Exponential are necessary for quantum computing. The role of Linear Algebra in Quantum Computing is depicted in the image below. Linear algebraic concepts are fundamental to all computations. You can find more information on the linear algebra required for quantum computing in this link (advanced concepts are covered).
Topics with broad applications in AI and QC have been the focus of several articles.
Linear Algebra introduces four important data structures and the operations performed on them: Scalars, Matrices, Tensors, and Tensor Products.
Authors:

Dr. Manish Bhardwaj
Department of Computer Science & Information Technology,
KIET Group of Institutions, Delhi-NCR, Ghaziabad, India

Ms. Shaili Singhal
Department of Computer Science & Information Technology,
KIET Group of Institutions, Delhi-NCR, Ghaziabad, India
